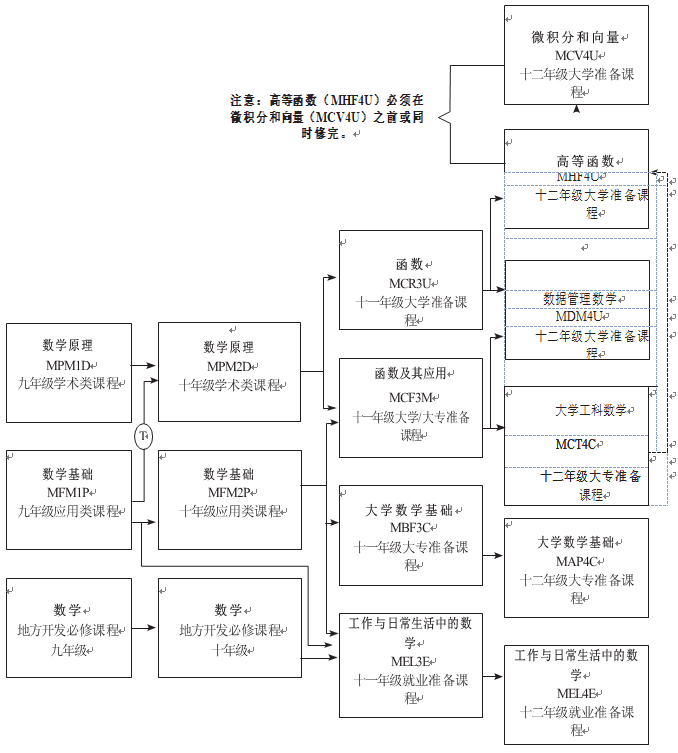
数学

数学原理，9年级学术类课程（MPM1D）

本课程能够使学生通过调查、有效运用技术和抽象推理，了解与代数、解析几何、测量和几何有关的数学概念。学生将研究关系，然后将其概括为线方程，并确定线性关系不同表示之间的联系。他们还将探讨因测量三维图形和二维形状而产生的关系。

在解决多步骤问题时，学生可用数学思维进行推理并表达自己的观点。

成功完成本课程的学生日后可进修10年级学术类课程数学原理（MPM 2D）或10年级应用类课程数学基础（MFM 2P）。本课程的重点之一是让学生学会抽象推理。

前置课程：无

数学基础，9年级应用类课程（MFM1P）

本课程能够使学生通过调查、有效运用技术和实操活动，了解与代数入门、比例推理、测量和几何有关的数学概念。学生将研究现实生活中的示例，以开发线性关系的各种表示形式，并确定这些表示形式之间的联系。他们还将探讨因测量三维物体和二维形状而产生的关系。

学生的数学技能也将得以巩固，使其能够有效解决问题和交流思想。

成功完成本课程的学生日后可进修10年级应用类课程数学基础（MFM 2P）。（注意：完成本课程后，如果学生希望转到10年级学术类课程数学原理（MPM 2D），则需要学习转换课程。）在动手实践中学习以及学会运用具体示例也是本课程的重点之一。

前置课程：无

地方开发必修课程，9年级（MAT1L）

本课程旨在深化学生的数学知识和技能，为学生成功应对日常生活、职场和10年级地方开发必修课程打下基础。

该课程包括三个部分：金钱意识、测量和比例推理。不论哪个部分，重点都是通过解决真实的日常问题来培养和巩固学生的基本数学概念和技能。

学生有机会进一步发展其数学素养和问题解决能力，并通过相关且实用的数学活动来加强其在阅读、写作和口语方面的技能。

前置课程：无

数学原理，10年级学术类课程（MPM2D）

通过本课程，学生可以根据调查、有效运用技术和抽象推理来加深对关系的理解，并深化其解决问题的能力和代数技能。学生将探析二次关系及其应用；解决和应用线性系统；使用解析几何验证几何图形的属性；并研究直角三角形和锐角三角形的三角学。在解决多步骤问题时，学生可用数学思维进行推理并表达自己的观点。

前置课程：数学，9年级学术类或应用类课程+转换课程

数学基础，10年级应用类课程（MFM2P）

通过本课程，学生可以根据调查、有效运用技术和实操活动来巩固对线性关系的理解，并深化其解决问题的能力和代数技能。学生将建立和绘制解析几何方程式；使用实际示例解决和应用线性系统；并探索和解释二次关系图。学生将研究相似的三角形、直角三角形的三角学以及三维图形的测量。学生的数学技能也将得以巩固，使其能够有效解决问题和交流思想。

前置课程：数学，9年级学术类或应用类课程

地方开发必修课程，10年级（MAT2L）

本课程旨在拓展学生的数学知识和技能，为学生成功应对日常生活、职场和11年级数学就业准备课程打下基础。

该课程包括三个部分：金钱意识、测量和比例推理。不论哪个部分，重点都是通过解决真实的日常问题来强化和拓展学生的基本数学概念和技能。

学生有机会拓展其数学素养和问题解决能力，并通过相关且实用的数学活动来加强其在阅读、写作和口语方面的技能。

前置课程：一个9年级数学课程的学分

函数，11年级大学准备课程（MCR3U）

本课程在线性关系和二次关系的基础上介绍了函数的数学概念。学生将研究离散函数和连续函数的特性，包括三角函数和指数函数；用数字、代数和图形表示函数；解决涉及函数应用的问题；并建立多项式和有理式的简化工具。在解决多步骤问题时，学生可用数学思维进行推理并表达自己的观点。

前置课程：数学原理，10年级学术类课程

函数及其应用，11年级大学/大专准备课程（MCF3M）

本课程在二次关系的基础上介绍了函数的基本特点。本课程的重点是二次函数、三角函数和指数函数以及它们在模拟现实情况中的运用。学生将用数字、图形和代数形式表示函数；简化表达式；解方程；以及解决与金融和三角函数应用有关的问题。在解决多步骤问题时，学生可用数学思维进行推理并表达自己的观点。

前置课程：数学原理，10年级学术类课程，或数学基础，10年级应用类课程

大学数学基础，11年级大专准备课程（MBF3C）

本课程旨在拓展学生对数学的理解，使其认识到数学是现实世界中解决问题的一把工具。学生将更广泛地了解二次关系、测量和几何；探析指数增长情况；解决复利问题；解决与车辆拥有量相关的财务问题；以及通过收集、分析和评估涉及一两个变量的数据来培养他们的推理能力。学生的数学技能也将得以巩固，使其能够有效解决问题和交流思想。

前置课程：数学基础，10年级应用类课程

工作与日常生活中的数学，11年级就业准备课程（MEL3E）

本课程旨在拓展学生对数学的理解，使其认识到数学也能应用于职场和日常生活中。通过本课程，学生将能够解决与赚钱、纳税和购物有关的问题，将单利和复利的计算运用到储蓄、投资和借款中，以及计算各种情况下的运输和旅行费用。学生的数学技能也将得以巩固，使其能够有效解决问题和交流思想。

前置课程：数学原理，9年级学术类课程，或数学基础，9年级应用类课程，或部委通过的地方开发的数学课程

高等函数，12年级大学准备课程（MHF4U）

本课程扩展了学生的函数体验。学生将研究多项式、有理式、对数算术和三角函数的性质；加深对变化率的理解；以及运用这些概念和技能开发工具。学生还将完善对数学过程的使用，以便顺利修完高级数学。不论是学生想在大学期间学习数学还是在学习任何一门大学课程前加深对数学的理解，本课程都适用。

前置课程：函数，11年级大学准备课程，或工科数学，12年级大专准备课程

微积分和向量，12年级大学准备课程（MCV4U）

本课程基于学生以前的函数体验以及对变化率的理解。通过本课程，学生将能够解决与向量几何和代数表达式以及三维空间线和平面表达式相关的问题；加深对变化率的理解，包括多项式、有理式、指数函数和正弦函数的导数；并将这些概念和技能应用于现实世界中的关系建模。学生还将完善对数学过程的使用，以便顺利修完高级数学。本课程适合计划在大学学习数学的学生，以及毕业后从事物理和工程等领域的学生。

前置课程：高等函数，12年级大学准备课程。注意：除前置课程外，某些学校可能还要求学生同时修完MCV4U课程。

数据管理数学，12年级大学准备课程（MDM4U）

本课程侧重数据管理方面，拓宽了学生对数学的理解。通过本课程，学生将掌握如何组织大量信息；解决概率和统计问题；并完成含统计概念和技能的毕业项目。学生还将完善对数学过程的使用，以便顺利修完高级数学。尤其那些计划在大学主修商业、社会科学和人文科学的学生会对这门课程特别感兴趣。

前置课程：函数及其应用，11年级大学/大专准备课程，或函数，11年级大学准备课程

大学工科数学，12年级大专准备课程（MCT4C）

本课程能够使学生更广泛地了解函数。学生将研究并应用多项式、指数函数和三角函数的特性；继续以数字、图形和代数方式表示函数；开发简化表达式和求解方程的工具；解决代数、三角学、向量和几何的应用问题。在解决多步骤问题时，学生可用数学思维进行推理并表达自己的观点。本课程为学生日后在大学学习工科课程打下基础。

前置课程：函数及其应用，11年级大学/大专准备课程

大学数学基础，12年级大专准备课程（MAP4C）

本课程旨在让学生了解数学在现实世界中的广泛应用。学生将使用统计方法分析数据；解决几何和三角学应用问题；简化表达式；求解方程。在解决多步骤问题时，学生可用数学思维进行推理并表达自己的观点。本课程为学生日后学习商业、健康科学和人类服务等大学课程以及从事某些技能行业打下基础。

前置课程：大学数学基础，11年级大专准备课程

工作与日常生活中的数学，12年级就业准备课程（MEL4E）

本课程旨在拓展学生对数学的理解，使其认识到数学也能应用于职场和日常生活中。学生将研究统计学使用问题；应用概率概念来解决熟悉情况下出现的问题；调查住宿费用并制定家庭预算；使用比例推理；估计和测量；以及应用几何概念来创建设计。

学生的数学技能也将得以巩固，使其能够有效解决问题和交流思想。

前置课程：工作与日常生活中的数学，11年级就业准备课程